David Smith, Joseph Myers, Craig Kaplan, and Chaim Goodman-Strauss have discovered an aperiodic monotile: a polygon that tiles the plane by rotations and reflections, but cannot tile the plane periodically.
Any tiling induced by the monotile is scalemic: the majority of tiles are unreflected, with only a relatively small proportion (shown in dark blue) being reflected. The ratio of unreflected to reflected tiles is φ^4 : 1, as can be determined from taking the authors’ description of the tiling in terms of a substitution system of ‘metatiles’:
- H → 3H + 3P + 3F + T
- P → 2H + P + 2F
- F → 2H + P + 3F
- T → H
and then taking the dominant eigenvector (corresponding to the dominant eigenvalue φ^4) to find the proportions of metatiles in the limit tiling, and using that to deduce the fraction of unreflected monotiles.
The tile itself is remarkably simple: it is a 13-sided polygon formed from the union of eight of the kites in the deltoidal trihexagonal tiling, which is itself the common refinement of the regular hexagonal tiling and its dual:
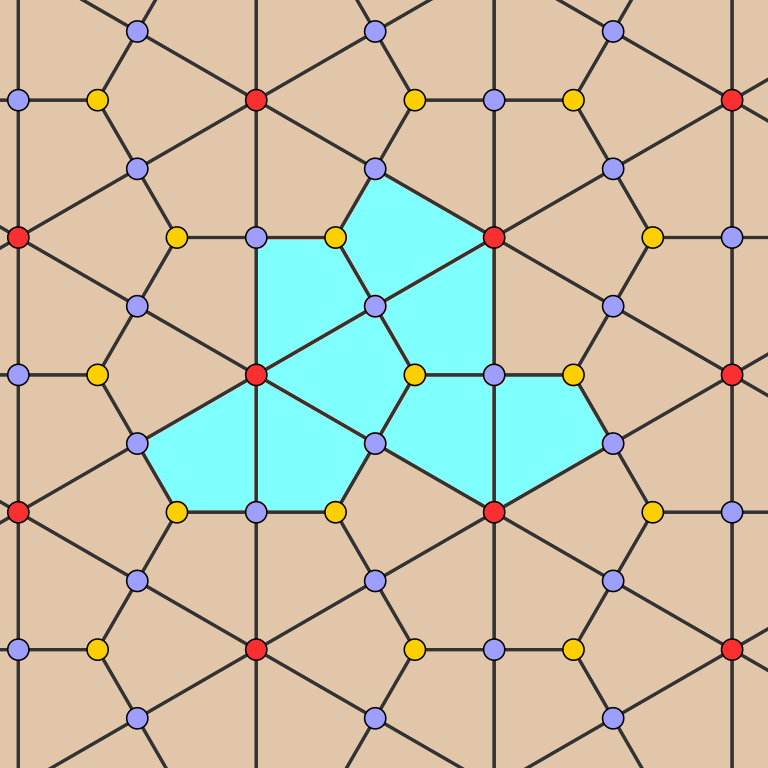
Adapted from an illustration by Tilman Piesk
This paper came a few days after the solution of another long-standing open problem in combinatorics, namely an improvement to the exponent in the upper bound on the Ramsey number R(s, s).
Additionally, a few months ago Barnabas Janzer proved that there exists a pair of convex compact sets 